The Uncertainty Principle

Is a particle a wave? Is a mango a line? Some things can never be known for certain.

Quantum  Physics has always been that one mysterious theory that has been really  difficult to understand. Richard Feynman, a noble prize winner in this  field once said:

“If you think you understand quantum mechanics, you don’t understand quantum mechanics”

Which is kind of demoralizing, ’cause if he didn’t understand it, what chance do we have? I think it has been so difficult to understand because almost  everything in the Quantum Realm, defies common sense, which makes it  really hard to comprehend the strange phenomenons taking place there.

Most  of us have a general idea of what the whole thing is about. But for  those of my friends that don’t, theoretical physics is mainly divided  into two parts: General Relativity and Quantum Mechanics.

General Relativity describes all the stuff that happens on a large measurable level (though it does get a bit too large at times). Things like space, the planets, the stars, and so on.

Quantum  Mechanics, on the other hand, covers the small, at the micro level. It  discusses how electrons behave, how light moves, and the behavior of all  those tinier-than-tiny micro-microscopic particles that we almost don’t  know about.

So  what exactly is Quantum Physics? Why do we need a separate theory for  this microscopic world? After all, these are the things that make up the  entire universe. In theory, our theories should work just fine there as  anywhere else.

In reality, however, they don’t.

When  you shrink an object to the size of an atom, gravity and light work  very, very differently. And many new forces such as the weak and strong nuclear force come into play, that have absolutely no effects up in the visible world.

Gravity  is a relatively weak force, which only seems stronger because it can  operate over large distances. When things are really close together,  like in the middle of an atom, then the other forces dominate. (And yes,  the ‘weak force’ is stronger).

Hold on a moment — do you know what an atom is? That’s an idea that might need changing.

Okay,  so I’m assuming that you have a basic idea of what “atomic particles” —  meaning electrons, protons, and the like — are. Tiny objects that sit  in the core of the atom or spin around it. Right?

I’m guessing you studied the Bohr’s Model, which looks somewhat like this:

According to this model, the negatively-charged electrons are circling around a positively charged nucleus.

Bohr  thought of these electrons as particles. Each particle has a specific  mass, is in a specific position, and moves along in a certain, specified  way.

But  with quantum physics, there’s nothing so certain and fixed. Because of  being so small, we can’t really see where subatomic particles are(I’ll  explain why), so for us, they exist in clouds (a place where their  existence probability is the highest) instead of a fixed place.

Cause  of them not really being particles(For us), Quantum physicists instead  of assuming them as particles and doing mathematical functions on them,  describe these subatomic particles using waves. So instead of a fixed  place where an electron might be, the position of an electron looks  something like this —

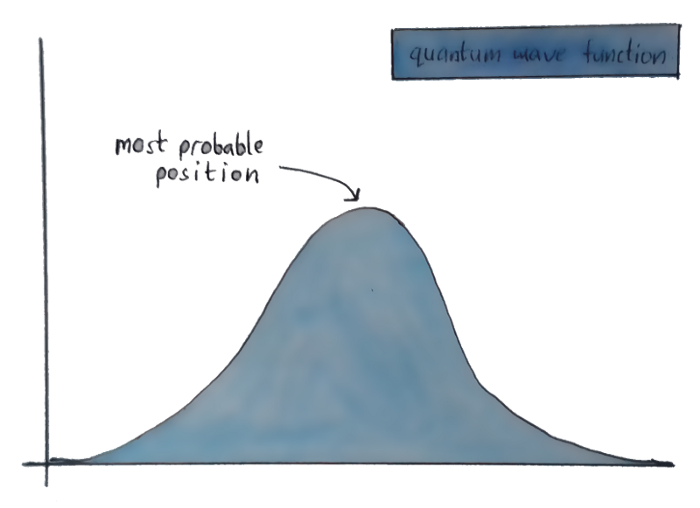
You don’t know where exactly the electron is, but the graph shows the different places it could be, and which of those places you’re most likely to actually find it.

Now,  just to be clear, this is not a physical wave like the ripples we see  in water or like the sound waves we’re familiar with. This is just an abstract mathematical wave, that gives us a mathematical description of an electron.

This wave comes as the solution to Schrodinger’s equation, which looks something like this —

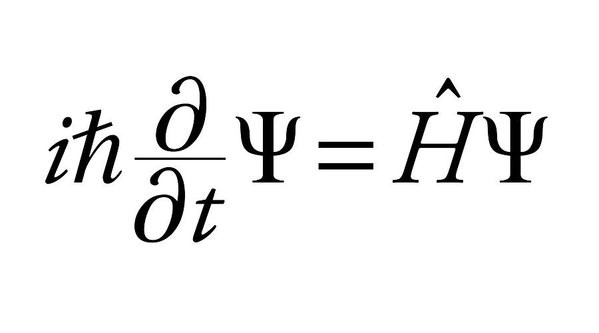
So yeah, you can see pretty clearly that it’s just math.

When  you solve this equation and plot the solutions on a graph, you get the  wave-function. This is very similar to the algebra you do in high  school, where you solve a quadratic equation and draw its wave on the  graph paper.

So if something uses wave-functions, isn’t it basically a wave? Not necessarily: the wave-function is just a graph.

Here’s another graph:

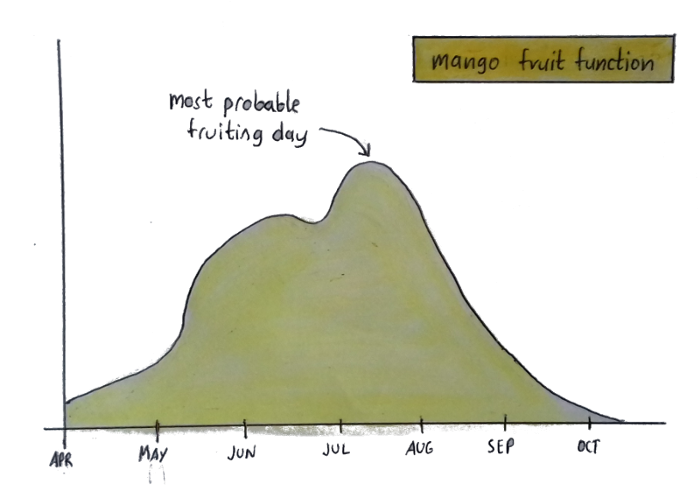
This  graph tells me how likely it is for my mango tree to fruit on a given  day. But that doesn’t mean my tree actually looks like a curvy line —  that’s just a visual depiction of when you can expect fruit.

In physics, when people say something “is a wave”, they usually mean it follows certain rules.

When  the hump, or “crest”, of a wave merges with another crest, they combine  to form an even bigger one. And if a crest comes in contact with a  valley, or “trough”, they cancel each other out. This combining or  canceling is called “interference”, and it works the same way whether  you’re looking at birds causing ripples on a telegraph wire or a music  melody floating through the air.

They  don’t necessarily do it the same way — telegraph wires swing up and  down, whereas music and other sounds are caused by compression of air —  but they still do it.

Electrons are not exactly wires or music, but their wave-like equations do come in pretty handy.

Suppose you want to calculate the position or momentum of the electron, you can easily do it using the wave function.

To  find the position of this electron, you take the “amplitude” of the  wave function, meaning how high it is from the baseline. Then you square  that and construct a new “wave” on a graph. That “wave” would give us  the probability distribution of finding the electron in that particular  place — which is to say, the list of places the electron could be, and  how likely it is to be in each.

Remember, I said probability.  In Quantum Mechanics we can’t know anything with absolute certainty. So  I can’t say for sure that the electron is now at the point with the  highest amplitude, but what I can say for sure is, it has the highest probability of being there.

Why  is Quantum Mechanics so fuzzy and un-exact? Well, after a point, it’s  literally impossible to measure things precisely. You can’t just see  where an object is, and here’s why.

To  see an object, we first have to look at it. That usually means you  shine some light on it, and shining light means bombarding it with  photons. Okay, so what’s the problem with this?

For  big objects like mice and footballs, shining light doesn’t really  matter. But on a smaller scale, it does. All light has energy, you see,  and when you’re a tiny electron going about your business, then a big  heavy photon smashing into you will surely throw you off the direction.

If you use light, you can measure where a particle was, but not where it’s going.

What  if you use less light? Well, there’s a limit to how less they can get.  You can’t send light in any arbitrary amount, but only in bundles of a  certain amount of energy. These bundles are what are called “photons”,  and you can’t have “half a photon”.

By  the way, I’m calling it “bundle” here, but the actual word is  “quantum”, or “quanta” if it’s many. And that, incidentally, is where  “Quantum mechanics gets its name.

So  you can’t know where a particle is without bumping it at least one  quantum’s worth out of the direction. But what if you use a smaller  quantum?

Not  all light-waves have the same amount of energy. A quantum of red light  has less energy than a quantum of blue because it vibrates less rapidly:  its frequency is lower.

The  problem is, lower-frequency light means wavelengths are much longer. So  you can figure out where a particle’s going because you won’t bump it  out of the direction, but your measurement as to where exactly it is will be imprecise. Longer wavelengths mean your reference points are  much farther apart: it’s like having a ruler with kilometers instead of  centimeters.

That’s  why things are so vague. That’s why things are so uncertain. And,  that’s why this thing is called Heisenberg’s Uncertainty Principle.

Werner  Heisenberg, who came up with the principle, didn’t exactly think of  photons and bumpings. He tried it using wave functions but came to the  same conclusion.

Theoretically,  you can find out where a particle is with the wave-function: just  measure the amplitude. You can also find its momentum: just measure the  wavelength. But imagine an electron having a random wave-function like  this one —

The  amplitude of this wave can be calculated easily and thus, the  probability of finding this electron at a particular point is known. (We  don’t accurately know its position, but let’s ignore that for a  moment).

Now, consider the wavelength of the wave.

Yes! exactly, this wave has no fixed wavelength, and because of this, we are not sure about its momentum.

What if you tweak the equation around to get a regular “sine wave”?

This  wave has a fixed wavelength, and also it is not difficult to find its  amplitude, but the problem here is that this wave doesn’t end anywhere.  So the electron has an equal probability of existing anywhere at any  point in the entire universe.

Using  different kinds of light, you can know either where a particle is, or  how it’s moving — but never both at the same time. It’s impossible to  know both with absolute certainty. Even with wave-functions, you get the  same result.

In a nutshell, the principle is —

“It is impossible to know simultaneously the exact position and momentum of a particle.”

The  more exactly you determine the position, the less you know of its  momentum — and vice versa. So at a particular time, we can’t calculate  both the position and momentum of the particle.

The  Uncertainty Principle had great philosophical implications. For the  first time in history, physics admitted that it could never know some  things accurately. That, however, is just the tip of the quantum  iceberg.

So if you think Heisenberg’s idea is the weirdest in the world — well, wait till part two and perhaps you won’t be so certain.

Quanta in a Nutshell: This article is one of a four-part series on quantum mechanics. Up next: double-slits, self-conscious particles, and why duality is like an elephant

Want to write with us? To diversify our content, we’re looking out for new authors to write at Snipette. That means you! Aspiring writers: we’ll help you shape your piece. Established writers: Click here to get started.